Um Guia de Bitmaps para IniciantesEscrito por Paul BourkeRenderizados e modelos de Peter Diprose e Bill Rattenbury
IntroduçãoEste documento serve como uma introdução elementar aos bitmaps, pois eles são usados em computação gráfica. DefiniçãoOs bitmaps são definidos como uma malha retangular regular de células chamada pixels, cada pixel contendo um valor de cor. Eles são caracterizados por apenas dois parâmetros, o número de pixels e o conteúdo da informação (profundidade de cor) por pixel. Existem outros atributos que são aplicados em bitmaps, mas são derivações desses dois parâmetros fundamentais. 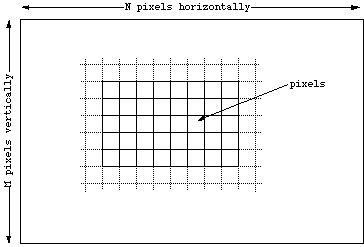
Observe que os mapas de bits são sempre orientados horizontalmente e verticalmente. Os pixels devem ser considerados quadrados, embora possam ter outros índices na prática.

Colour "depth"Cada pixel em um bitmap contém certas informações, geralmente interpretadas como informações de cores. O conteúdo da informação é sempre o mesmo para todos os pixels em um bitmap específico. A quantidade de informações de cores pode ser qualquer que seja o requerimento, mas existem alguns padrões, os principais são descritos abaixo. 1 bit (preto e branco)
Este é o menor conteúdo de informação possível que pode ser mantido para cada pixel. O mapa de bits resultante é arbitrado como monocromático ou preto e branco. Os pixels com um 0 são arbitrados como negros, pixels com 1 são arbitrados como brancos. Observe que, embora apenas dois estados sejam possíveis, eles podem ser interpretados como duas cores, 0 é mapeado para uma cor, 1 é mapeado para outra cor. 8 bit greys
Neste caso, cada pixel leva 1 byte (8 bits) de armazenamento, resultando em 256 estados diferentes. Se esses estados forem mapeados em uma rampa de cinzas de preto para branco, o bitmap é arbitrado como uma imagem em escala de cinza. Por convenção 0 é normalmente preto e 255 branco. Os níveis de cinza são os números entre, por exemplo, em uma escala linear 127 seria um nível de cinza de 50%. 
Em qualquer aplicação específica, o intervalo de valores de cinza pode ser qualquer coisa, é mais comum mapear os níveis 0-255 em uma escala de 0-1, mas alguns programas irão mapeá-lo em uma escala 0-65535 (veja o sistema de especificação de cores de maçãs como um exemplo). 24 bit RGB
Este é o próximo passo de 8 bit cinza, agora há 8 bits alocados para cada componente vermelho, verde e azul. Em cada componente, o valor de 0 refere-se a nenhuma contribuição dessa cor, 255 refere-se a contribuição totalmente saturada dessa cor. Uma vez que cada componente tem 256 estados diferentes, há um total de 16777216 cores possíveis. 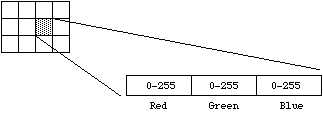
Essa idéia de espaço de cores RGB é um conceito fundamental em computação gráfica. No espaço RGB, qualquer cor é representada como um ponto dentro de um cubo de cores com eixos ortogonais r,g,b. 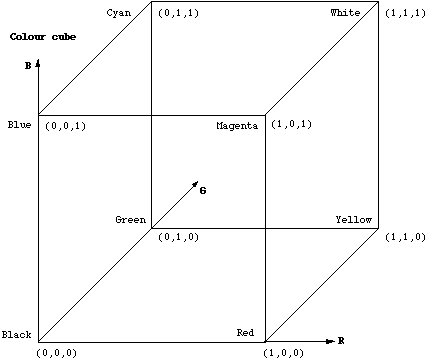
Observe que os valores de cinza formam uma linha direta de preto a branco ao longo da diagonal do cubo, r = g = b. Cor indexada de 8 bits
A cor indexada é uma maneira mais econômica de armazenar bitmaps a cores sem usar 3 bytes por pixel. Tal como acontece com bitmaps cinza de 8 bits cada pixel tem um byte associado a ele apenas agora o valor nesse byte não é mais um valor de cor, mas um índice em uma tabela de cores, chamado paleta ou tabela de cores. 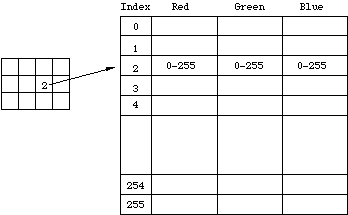
Existem vários atributos interessantes de um sistema de indexação de cores. Se houver menos de 256 cores na imagem, este bitmap será a mesma qualidade que um bitmap de 24 bits, mas pode ser armazenado com um terço dos dados. Os efeitos interessantes de coloração e animação podem ser conseguidos simplesmente modificando a paleta, isso muda imediatamente a aparência do bitmap e com um design cuidadoso pode levar a mudanças intencionais na aparência visual do bitmap. Uma operação comum que reduz o tamanho dos mapas de bits grandes de 24 bits é convertê-los em cores indexadas com uma paleta otimizada, ou seja, uma paleta que melhor representa as cores disponíveis no bitmap. Cor indexada de 4 bits
Isso é idêntico à cor de 8 bits, exceto que agora apenas metade de um byte, são utilizados 4 bits para o índice. Isso suporta uma tabela de até 16 cores. 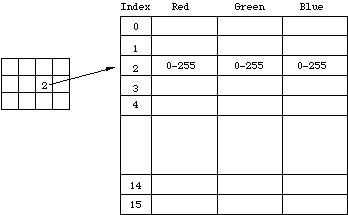 32 bit RGB
Isso é normalmente o mesmo que a cor de 24 bits, mas com um bitmap extra de 8 bits conhecido como um canal alfa. Este canal pode ser usado para criar áreas mascaradas ou representar transparência. 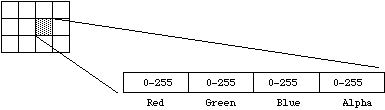 16 bit RGB
Este é geralmente um sistema direto com 5 bits por componente de cor e um canal alfa de 1 bit. 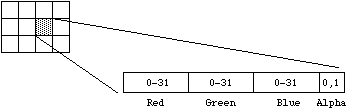
ResoluçãoA resolução é um atributo de um bitmap que é necessário ao visualmente visualizar ou imprimir bitmaps porque os pixels, por si só, não possuem dimensões explícitas. A resolução normalmente é especificada em pixels por polegada, mas pode ser em qualquer outra unidade de medida. A maioria dos processos de impressão retém unidades de pixels por polegada (DPI) por motivos históricos. Em dispositivos com nn pixels retangulares a resolução pode ser especificada como dois números, a resolução horizontal e vertical. O conceito de resolução sendo independente do conteúdo de informação de um bitmap é muito importante, dada uma profundidade de cor constante, então o conteúdo de informações entre diferentes mapas de bits é apenas relacionado ao número de pixels verticalmente e horizontalmente. A qualidade no entanto, quando o bitmap é exibido ou impresso depende da resolução. Uma vez que a resolução determina o tamanho de um pixel, ele também pode ser usado para modificar o tamanho da imagem geral. Como exemplo, considere um bitmap que é 200 pixels horizontalmente e 100 pixels verticalmente. Se este bitmap foi impresso em 100DPI, ele medirá 2 polegadas por 1 polegada. Se no entanto, o mesmo bitmap foi impresso em 200 DPI, então ele só medeia 1 polegada por meia polegada. 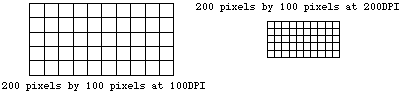
Sempre que um mapa de bits é exibido em um monitor de computador, a resolução precisa ser considerada. A maioria dos monitores de computador tem uma gama de resolução de 60DPI na resolução baixa para 120DPI para monitores de alta resolução. Quanto ao material impresso, quanto maior a resolução, menos aparente será a natureza do pixel do bitmap.. Como outro exemplo, as duas imagens a seguir são idênticas no conteúdo da informação; no entanto, elas têm resoluções diferentes e, portanto, diferentes tamanhos de pixels. O menor é 80DPI e o maior é o 30DPI. Os pixels são muito mais evidentes na versão maior. 
Esta não é toda a história quando se trata de representar mapas de bits em dispositivos físicos porque os diferentes dispositivos possuem capacidades de profundidade de cores diferentes. Conversão de profundidade de cor.Muitas vezes é necessário representar um bitmap com uma profundidade de cor em um dispositivo com diferentes capacidades de profundidade de cor. Claro, se o dispositivo de destino tiver uma cor melhor do que o bitmap, então não há problema, pois o bitmap pode ser representado exatamente. Na situação inversa em que o destino possui capacidades diferentes e menores, o bitmap deve ser convertido em algo que ofereça a melhor representação possível. Como exemplo, considere o problema de representar imagens em escala de cinza em dispositivos monocromáticos (preto e branco). Isto é conseguido usando um número variável de pixels em preto e branco para representar um nível de cinza. Felizmente, o dispositivo preto e branco geralmente tem uma resolução muito maior do que o bitmap, portanto há uma série de pixels disponíveis para criar a aproximação em escala de cinza. Considere um mapa de bits de escala de escala 75DPI para ser exibido em uma impressora a preto e branco 300DPI. Existe uma matriz de pixels 4x4 preto e branco que podem ser usados para representar cada pixel de escala de escala. 
Há uma série de técnicas que podem ser usadas para formar a disposição correspondente de pixels em preto e branco, uma técnica é chamada de dithering. Mesmo usando dithering, existem muitos algoritmos possíveis para decidir o arranjo de pixel com dither. O seguinte mostra uma rampa de nível de cinza com os exemplos negativos em preto e branco correspondentes (amplamente ampliados) usando padrão e difusão dithering. 
Como já mencionado, existem outros métodos de conversão de bitmaps de alta profundidade de cor para aquelas de menor profundidade de cor, mas maior resolução, sobre a técnica utilizada na indústria de impressão é chamada de triagem. O rastreio não será discutido aqui, exceto para dizer que ele se aproxima dos níveis de cinza por objetos de tamanho diferente (o tamanho do objeto é proporcional ao nível de cinza). Os objetos são dispostos em uma matriz normal que está em algum ângulo com a horizontal. Os objetos de imagem mais comumente usados são pontos, linhas e retângulos. O seguinte mostra uma rampa de nível de cinza com os exemplos correspondentes em preto e branco (amplamente ampliados) usando telas de ponto e linha. 
A discussão acima e os exemplos de conversão de profundidade de cor foram feitos com respeito a imagens em escala de cinza. A conversão de imagens de profundidade de alta cor para representações de baixa profundidade de cor não é diferente no conceito, geralmente o processo é feito apenas três vezes, um para cada componente de cor. Armazenamento BitmapA maneira mais direta de armazenar um bitmap é simplesmente listar as informações de bitmap, byte após byte, linha por linha. Os arquivos armazenados por este método geralmente são chamados de arquivos RAW. A quantidade de armazenamento em disco necessária para qualquer bitmap é fácil de calcular, dado as dimensões do bitmap (N x M) e a profundidade de cor nos bits (B). A fórmula para o tamanho do arquivo em KBytes é 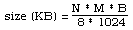
onde N e M são o número de pixels horizontais e verticais, B é o número de bits por pixel. A tabela a seguir mostra os tamanhos de arquivo de alguns tipos de bitmap se eles estiverem armazenados no Formatoo RAW. image dimensions colour depth file size
128 x 128 1 bit 2 KB
8 bits 16 KB
24 bits 48 KB
256 x 256 1 bit 8 KB
8 bits 64 KB
24 bits 192 KB
1K x 1K 1 bit 128 KB
8 bits 1 MB
24 bits 3 MB
Como pode ser visto a partir desta tabela, grandes imagens de 24 bits resultarão em arquivos muito grandes, é por isso que a compactação torna-se importante. Há um grande número de Formatos de arquivo usados para armazenar bitmaps compactados do trivial para o muito complicado. Os Formatos complicados existem por causa dos arquivos de bitmap muito grandes que existiriam se a compressão não fosse usada. Existem duas grandes categorias de Formatos de arquivos compactados, aqueles que são sem perdas (retém os mapas de bits perfeitamente) e aqueles que estão com perdas. O seguinte mostra a hierarquia principal das técnicas de compressão. 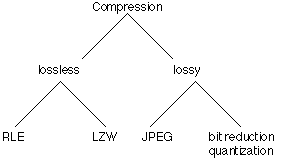
A maneira mais difícil de reduzir o tamanho dos arquivos de bitmap é reduzir as informações de cores, isto é chamado de redução de bits ou quantização. Por exemplo, pode-se converter bitmaps de 24 bits em bitmaps de 8 bit indexados usando dithering para simular as cores perdidas. O Formatoo de perda mais comum, de longe, é JPEG, uma descrição de como funciona está bem fora do escopo desta discussão. Sua principal vantagem é que ele pode oferecer taxas de compressão muito melhores do que os Formatos sem perdas. Por exemplo, considere o seguinte bitmap, cujo original é de 500 x 350 pixels na cor de 24 bits. Usando a fórmula fornecida anteriormente, o tamanho do arquivo não comprimido é 500 x 350 x 24/8/1024 = 513K 
Salvo em escala de cinza (redução de profundidade de bit), o arquivo é 171K (3 vezes menor), salvo e compactado usando
RLE é 388K (75% do original), salvo usando a compressão LZW é 188K (36% do original), salvo como JPEG é 30K (uma taxa de compressão de 17: 1). 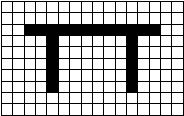
Se isso fosse armazenado em forma RAW, precisaria de 16 bytes por linha para as 10 linhas. No entanto, as duas primeiras linhas são todas do mesmo nível, por isso é mais eficiente simplesmente salvar o número das mesmas cores em uma corrida junto com a cor da execução. As duas primeiras linhas em vez de precisar de 16 bytes só precisam de 2 bytes cada. No Formatoo bruto, as três primeiras linhas seriam 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 0 0Usando a codificação de comprimento de execução, as três primeiras linhas seriam
16 0 16 0 2 0 12 1 2 0 Embora existam mais detalhes envolvidos nas implementações reais de RLE do que descrito aqui, este é o princípio básico por trás da codificação do comprimento de execução. Para que o RLE obtenha algum grau de compressão, é necessário que haja corridas da mesma cor, por isso é improvável que seja útil para imagens altamente coloridas, como fotografias de 24 bits. |